bases de la mécanique céleste
![]()
| Les lois de l'univers | Documents pédagogiques | Page d'accueil "Astronomie" |
|
|
Première loi de KEPLER : | |
|
Les planètes tournent autour du Soleil en suivant des orbites en forme d'ellipse dont le Soleil occupe un des foyers. Tous les corps en orbite autour du Soleil suivent cette loi. Les planètes ont en général des orbites peu excentriques, parfois même quasiment circulaire. Les comètes et certains astéroïdes, par contre, ont souvent des orbites elliptiques très excentriques (et donc très "aplaties"). Les satellites, qu'ils soient naturels ou artificiels, suivent aussi des orbites elliptiques "képlériennes". La Lune, le télescope spatial Hubble ou l'ISS, entre autres, sont satellites de la Terre. Leurs trois orbites ont un foyer commun, le centre de gravité de notre planète. |
||
|
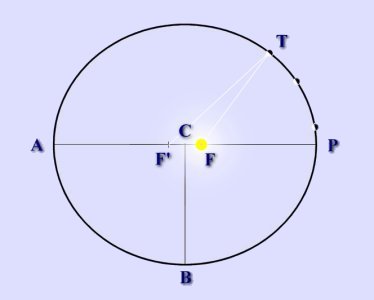
Le trajet de la Terre autour du Soleil.
F et F' : les deux foyers de l'ellipse. Le Soleil est en F. C : Centre géométrique de l'ellipse P : Périhélie (2 janvier) A : Aphélie (5 juillet) T : Terre Deux grandeurs définissent la forme de l'ellipse : son demi-grand axe : AC ou CP = a et son excentricité : e = CF / a pour la Terre, e=0,0017 et a=1 UA soit 149 597 870 km Les autres caractéristiques de l'ellipse en sont déduites. Demi-petit axe : 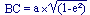
Distance au périhélie : 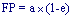
Rayon vecteur : 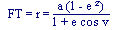
où "v" est l'angle PFT. |
|
|
Un peu de géométrie à propos de l'ellipse. Une ellipse est une courbe plane fermée, possédant deux foyers. En sciant un tuyau rond en oblique, on génère une ellipse. L'ombre d'un objet plat et circulaire (pièce de monnaie, CD-ROM) présente facilement une forme elliptique. On peut définir complétement une ellipse en donnant seulement deux valeurs : la longueur de son demi-grand-axe (a) et son excentricité (e). |
||
|
Pour tracer une ellipse de demi-grand axe a et d'excentricité e, on peut utiliser une ficelle de longueur 2a fixée à deux punaises écartées de 2a fois e (les foyers F et F'). Tendez la ficelle avec un crayon et vous tracerez facilement l'ellipse. 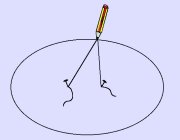
Lorsque les deux foyers sont confondus (cas de e=0), l'orbite est un cercle parfait (orbite circulaire), son excentricité est égale à zéro.
|
||
| Deuxième loi de KEPLER, dite loi des aires : | ||
|
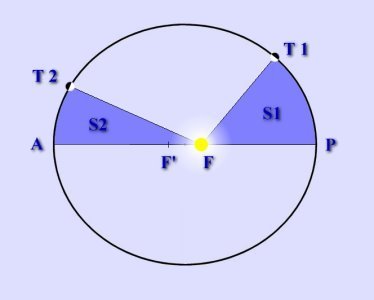
Les aires balayées par le rayon vecteur d'une planète sont proportionnelles au temps. Le rayon vecteur est le segment de droite qui relie la planète au Soleil, sa longueur est variable. Les deux triangles curvilignes F-P-T1 et F-T2-A ont la même surface, soit S1 = S2. La 2ème loi de Képler implique que ces surfaces, étant égales entre elles, ont été balayées en des temps égaux. La planète a donc mis le même temps pour aller de P à T1 que pour aller de T2 à A. Comme on peut le constater, la distance P-T1 est plus grande, donc la vitesse moyenne sur ce trajet est plus élevée. La planète a donc une vitesse variable sur son orbite, suivant l'endroit de celle-ci où elle se trouve. Elle est plus élevée au périhélie (point P) qu'à l'aphélie (point A). |
||
|
La vitesse de la Terre autour du Soleil.
S1 = S2 : les deux triangles curvilignes ont des surfaces égales. P : Périhélie (2 janvier) A : Aphélie (5 juillet) T1 et T2 : Deux positions de la Terre Les distance P-T1 et T2-A étant parcourues dans le même temps, les vitesses moyennes sur ces deux trajets sont différentes. |
|
| Troisième LOI DE KEPLER | ||
|
Pour toutes les orbites planétaires le rapport du carré des périodes de révolution (p) au cube du demi-grand-axe de l'orbite (a) est constant. 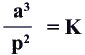
On peut exprimer a en Unités Astronomiques (en abrégé UA, 1 UA = 150 000 000 km) p en années K est une constante La troisième loi de KEPLER s'applique aussi, avec la même valeur de K, aux astéroïdes et aux comètes du système solaire. 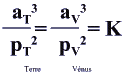
On peut l'appliquer à un ensemble de satellites orbitant autour d'une planète, comme Jupiter ou Saturne, entre autres, mais en redéfinissant la valeur de K pour chacun des systèmes. La troisième loi de KEPLER permet, connaissant la valeur de K et la période de révolution d'un astre, de calculer sa distance. |
||
| Application pour de petits calculs sur la comète de Halley | ||
| Deux feuilles format A4, détaillant des calculs d'application ultra-simples et permettant de tracer l'orbite de la comète de Halley. | ||
 Feuille de calcul A4 (fichier .pdf de 8 ko) |
 Feuille de tracé A4 (fichier .pdf de 13 ko) |
|
|
|
||
| Les lois de l'univers | Documents pédagogiques | Page d'accueil "Astronomie" |